无名氏定理简介
无名氏定理(Folk Theorem)即在重复博弈中,只要博弈人具有充足的耐心(贴现因子充足大),那么在满足博弈人个人理性约束的前提下,博弈人之间就总有多种或许促成合作均衡。存在无穷多对有限自动机策略,可以形成无限重复博弈的平衡点,并同期达到双方的合作。无名氏定理之所以得名,是受于重复博弈促进合作的思想,早就有很多人提出,以致无法追溯到其原创者,于是以“无名氏”命名之。
我们知道,单凭理性计算,有限次重复博弈,是处理个体理性与集体理性之间冲突的。在无限重复博弈中,举动规则可以用自动机来代表,于是不同举动规则的相争,便成了机器与机器的角斗。如果甲和乙玩无限重复的囚犯博弈。甲相信《美德的起源》一书作者的教导,认定仁厚忠恕既高尚又有效,于是以它为策略。乙信奉理性流氓主义,崇尚实力和实利,于是以流氓主义为策略。如此,二人间的博弈,就可以看作恕道机器与流氓机器的争斗。我们可以推演出各个回合双方的举动如下:第一回合,甲仁厚玩合作H,乙宰客玩欺骗D;第二回合,甲报复玩欺骗D,乙依然宰客玩欺骗D;第三回合,甲仍报复玩欺骗D,乙发现甲并不是傻客,于是玩合作H;第四回合,甲原谅乙,玩合作H;乙却因甲上次不合作,回头玩欺骗D宰客;……这样等等。整个结果序列如下图所示:
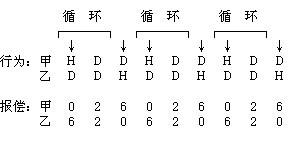

请注意,此序列呈现一个有趣的规律:就是每三个一组,持续循环重复。于是我们很容易算出,博弈各方平均每个回合的报偿有多少,只要取陆续三个回合,作个简单平均就够了。甲得到(0+2+6)/3= 2.67,乙得到(6+2+0)/3= 2.67 。显然,两者平分秋色,不相上下,谁也不比谁差,谁也不比谁强。
该种循环重复并没有是特殊情况。可以证明,有限自动机玩无限重复博弈,其结果最终全将变成循环重复序列。于是,利用相似的办法,我们可以针对下表中列出的七种策略,算出每一对策略相博所造成的的平均报偿。这些报偿可以写成一个7×7博弈矩阵,如下表所示(其中一部分略去了小数,这不影响下面的讨论):
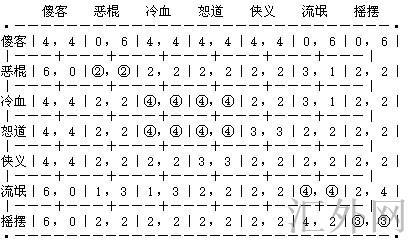

( 纵轴为甲,横轴为乙)
上面这个表里面,有带圈数字的格子均为平衡点。比如,乙玩恶棍策略时,甲无论玩什么,都不比当恶棍导致的好处许多,顶多不致受损而已。所以,甲乙双方都当恶棍,次次都玩欺骗,便是重复囚犯博弈的平衡点之一,此时各方的报偿与一次性博弈相同,均为2。
观察一下上面这个表,我们会发现它有多个平衡点。非重复博弈中的均衡点,恶棍对恶棍,双方永远玩欺骗,依然是无限重复博弈的均衡点。无条件合作的傻客策略,依然不是重复博弈的均衡点,理性的人,决不会当傻客。更重要的是,重复博弈引进了很多新的平衡点,其中有不少平衡点,可以达到合作报偿(4,4)。这包含恕道策略对恕道策略,恕道策略对冷血策略,冷血策略对冷血策略,流氓策略对流氓策略等,都可以保持双方的合作。以流氓对流氓为例:第一回合,双方耍流氓互宰,发现对方不是好惹的之后,双方转入合作心态,此后一直保持合作,如此无限次重复,其平均报偿均为4。实际上,存在无穷多对有限自动机策略,可以形成无限重复博弈的平衡点,并同期达到双方的合作。这就是有名的“大众定理(Folk Theorem)”,又译作“无名氏定理”。它之得名,是受于重复博弈促进合作的思想,早就有很多人提出,以致无法追溯到其原创者,于是以“无名氏”名之。
大众定理表明了举动规则的多样性:有无穷多种举动规则可以支持合作举动。在正常的平衡状态中,可观察到的举动可以完全相同的,此即博弈双方相互合作,不玩欺骗。但其后面的举动规则却或许大不相同合作,可以是受于双方都信奉仁厚的恕道主义,也或许是由于双方均为理性;流氓,还或许是由于双方都一冷血报复作威胁。这些举动规则上的区别,在正常的平衡状态中,是看不出来的,只有在非正常情形下,或在同外人的交往中,才会表现出来。为表明此点,设想有两个相互隔离的社会:一个形成了理性流氓式的举动规则,一个形成仁厚恕道的举动规则,他们各自内部都能保持相互合作,这形成了社会的正常状态。外人但凭观察这两个社会中民众的正常举动,看不出他们有什么区别。当下如果两个社会打破隔离,相互接触,会造成甚么情形?两套举动规则间会显现激烈的矛盾!
初次接触,流氓主义者将把对方当傻客,大宰其客。恕道主义者如果对方是好人,选择合作,导致在吃了亏之后,才以回宰其客相回报。流氓主义者见对方回宰,以为对方也是跟自己一样的流氓,于是转向合作心态,同期预期对方也选择合作。但恕道主义者依据“以直报怨”的原则,依然以宰客回报对方上次的欺骗。流氓主义者一看对方不合作,怒从心起,于是报之以宰客,这样循环往复,双方永远无法促成合作。
举动规则的矛盾,相似于人文学科里常说的文化矛盾。受于举动规则反应了民众对各自举动的平稳预期,一部分博弈论者把不同的举动规则解释为不同的文化信仰,应该是不无道理的。重复博弈理论,为我们科学理解很多文化现象,打开了大门。



