套期保值比率(Hedge Ratio)
套期保值比率的概念
套期保值比率是指为规避固定收益债券现货市场风险，套期保值者在建立交易头寸时所确定的期货合约的总价值与所保值的现货合同总价值之间的比率。确定合适的套期保值比率是降低交叉套期保值风险，高达最佳套期保值效果的核心。
套期保值比率计算公式
受于固定收益债券的票面利率有很多种，且大都不等于利率期货合约的标的资产(一般均为虚拟券)规定的利率。所以，在运用利率期货对固定收益债券执行套期保值时，固定收益债券现货的价值与所需利率期货合约的价值之间并没有是1：1的关系，规避等量不同品种债券的利率风险时，在利率期货市场上需要不同面值的期货头寸。而且基差风险的存在，会让套朗保值的效果承受很大影响，运用套期比率的概念，套期保值者能够尽或许地减弱基差风险的影响。用利率期货执行套期保值的目的是减弱利率变动对固定收益债券资产价格的影响，减弱利率风险。所以在完美套期保值下，现货头寸价格波动的损失应恰好为期货头寸的盈利冲抵，即：套期保值债券价格波动＝期货合约价格波动×套期保值比率
自此可得套期保值比率的计算公式：
ing="0" cellpadding="0" border="0">套期保值比率＝
所以，套期保值比率应当等于现货价格变动程度与期货标的单价变动程度的比。假使套期保值债券的波动大于所用来执行套期保值期货合约的波动，那么套期保值比率应大于1。
譬如，假定长期国债期货合约的标的债券是票面利率为3％的7年期虚拟国债，假使我们持有的债券票面利率为2.5%，期限是10年，那么同国债期货标的对比，该债券票面利率更高，期限更长，所以该债券价格受利率改变影响的程度更大，套期保值比率应大于1，即能够用较少数量的国债期货合约执行套期保值。假使债券价格波动性是期货标的波动性的两倍，那么每一单位的现货债券需要两倍金额的国债期货合约来为其保值。
套期保值比率的计算
确定利率期货套期保值比率最重要的原因是套期保值债券与利率期货合约波动的计算。在债券分析中，衡量债券波动性的指标首要有久期和基点价值，相应地，利率期货套期保值比率的计算方法有修正久期(duration)法、基点价值法(一)修正久期法1.久期久期是衡量债券持有者收到全部现金付款的平均等候时间，反应了债券价格与市场利率变动的关系，是衡量债券对利率敏感性的重要指标。当市场利率发生波动时，债券价格绝对波动程度与久期成正比，久期越大，价格波动就越大。在其余条件不变的情形下，债券期限越长，票面利率越低，久期越大。久期的概念最初是由Macaulay提出的，随后发展出多种不同的形式的久期，其中有麦考利久期(Macaulay duration)、修正久期、有效久期和核心年久期等。在假定收益率曲线平坦，而且用于所有将来现金流的贴现率固定不变的情形，麦考利久期的计算公式为：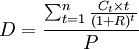
其中，D代表麦考利久期，t代表距偿还利息和(或)本金的时间长度，Ct代表在时间t偿还的利息和(或)本金，n代表债券到期日的时间长度，R代表利率，P代表债券贴现价格。其计算公式为：
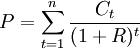
债券的现值是将来所有本息的现值，所以，久期是债券本息偿还时间的加权值，对应于t时的权重等于c时刻所有偿还的本息现值占债券总现值的比率。在对现货头寸执行套期保值时，投资人关心的是利率变动对债券价格变动的影响。将上面债券价格公式有关利率及求导数：
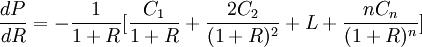
上式反应了利率发生微小变动时，债券价格的变动值。公式右边括号中恰好是债券的麦考利久期。将公式两边同除以债券价格P，就可得到利率发生微小变动时，债券价格变动的百分比，即：
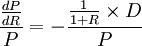
麦考利久期与(1+R)的比值一般称为修正久期(modified duration,Dm)：
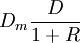
这显示，修正久期可以看做利率发生微小变动时所引起的债券价格的变动水平。
对于债券组合来说，其久期可以表明为组合中每只债券久期的加权平均，权重等于各债券在组合中所占的比重，这可以用久期的计算公式推导得到。
2.利用久期计算套期保值比率
久期度量了债券价格随利率变动时的波动特质，所以可以用来计算利率期货套期保值比率。受于利率期货合约价格近似等于最便宜可交割债券价格除以转换因子，所以利率期货合约的修正久期可以用最便宜可交割债券的修正久期除以转换因子得到。进而我们可以计算出最优的套期保值比率：
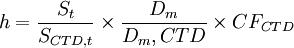
2002年3月份市场情形
利用修正久期法计算的套期保值比率为：
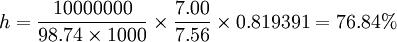
2002年3月份市场情形
所以，该基金经理在3月中旬以CHFl20．50的单价买进77张2002年6月到期的CONF期货合约。到5月中旬，市场利率果然下滑，债券价格上升(见上表)。于是该基金经理以每张合约CHN23．27的单价将持有的CONF期货合约平仓，并在债市上买回价值CHFl0210 000的债券组合。结果该基金经理在期货市场上所获利润不仅弥补了在债券上的亏损，而且仍有盈余CHF3290，套期保值是成功的(见下表)。
策略逻辑与结果
(二)基点价值法
除了久期外，其他衡量债券价格波动性的指标就是基点价值(basi。pointvalue，BPV)，即债券收益率改变一个基点(0．01个百分点)时，债券价格的改变程度(这里的改变程度指的是价格的变动额，并非是百分比)。即：
ing="0" cellpadding="0" border="0">债券基点价值＝
套期保值比率＝
=
ing="0" cellpadding="0" border="0">/
ing="0" cellpadding="0" border="0">=
ing="0" cellpadding="0" border="0">期货合约BPV＝
套期保值比率＝
2002年3月份市场情形
利用基点价值法计算的套期保值比率为：
h=\frac{32800.00}{0.06763\times1000}\times0.897383=435.22
2002年5月份市场情形
所以，该机构投资人持有债券组合可以通过在3月份以EUR106.00的单价出售435张6日到期的欧洲债券组合期货合约即可高达保值的目的。到5月份，利率果然上涨，债券组合价格下挫(5月的市场情形见上表)。于是改投资人出售所有的债券组合，同期以EUR103.73买进435张欧洲债券期货合约，将持有的期货合约对冲。结果。该投资人在债券结果上的损失在期货市场上得到了弥补(见下表)
策略逻辑与结果
套期保值比率的调整
分别用债券价格对利率变动的敏感性和对利率期货合约价格的敏感性推导出了套期保值比率的计算公式。在这一过程中，隐含着如此一个假定：最便宜可交割债券与被套期保值的债券之间的相对收益率差额是常数。我们并没有考虑各种债券本身的其余特点，尤其是在对不可交割债券执行套期保值时，被套期保值债券与最便宜可交割债券的一部分不同特性如信用等级、利率环境、期限特质等，会让得二者收益率之间的差额处在持续的变动当中，这将对套期保值的效果造成不利影响。所以，为保证套期保值的效果，在事实应用中，需要对前面计算得到的套期保值比率依照被套期保值债券的特质执行适当调整。
对利率期货套期保值比率执行调整的常用方法是收益率；系数法。具体做法是，用历史报告建立被保值债券收益率与最便宜可交割债券收益之间的回归方程：
rb = α + βrCTD + ε
其中，rb表明被套期保值债券的收益率，rCTD表明套期保值的CTD债券的收益率，ε是误差项，α和β分别是截距和回归系数。
利用回归分析可以得到系数β的预期值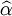
，称为收益率；(Yield beta)，表明被套期保值债券与CTD债券收益率间的相对变动率，即被套期保值债券收益率受CTD债券收益率变动的影响程度。误差项表明这两种债券收益率之间的关系不是固定的，是有噪声的。
利用收益率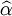可以对套期保值比率执行调整，以清除被保值债券因信用风险等原因而产生的与CTD债券收益率之间的差异。
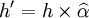其中，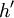
表明调整后的套期保值比率，h表明用修正久期法或基点价值法计算的套期保值比率。