随机规划与随机控制ALM模型(Stochastic Programming or Stochastic Control ALM Model)
随机规划与随机控制ALM模型简介 当前的ALM模型逐渐增多地运用到随机规划或随机控制的方法。 (一)随机规划模型首要是通过运用事件树、生成场景等元素,来为金融机构的资金配置供应一个描述将来资产价格、收益和风险等不确定原因在某种几率条件下的变动趋势的分析框架。金融机构在处理资金配置中会面对复杂的制约条件,受于随机规划模型和方法接纳了一部分更靠近于现实的如果,并给予了一种动态方法来处理多期资金配置中的困难,所以它可以在一个框架中同期处理交易成本、多元状态变量、市场不完全性、税收和交易制约、监管制约、公司政策要求等多原因困难,进而为金融机构大批量地处理和分析多种不确定原因的影响给予了机会。 国外金融学者对多期随机规划模型在金融机构的事实运用执行了大批的研究,并获得了很多成果。比如,布拉德里(Bradley)和克朗斯(Crane)于1973年,库斯(Kusy)和茨姆巴(Ziemba)于1986年为银行的ALM设计出了随机线性规划模型;马尔维(Mulvey)和瓦拉迪米罗(Vladimirou)于1992年为金融机构的资产配置提出了一个多期随机网络模型;卡里罗等(Carino et al.)于1994年为一家日本保险公司的资产负债管理困难构造了一个多期随机线性模型;希勒(Hiller)和厄可斯腾(Eckstein 1993),泽尼尔斯(Zenios 1993),古拉伯等(Golub et al 1993)则在20世纪90年代中期分别为固定收益证券管理构建了不同的随机规划模型。 其中公认比较有代表性的应当当属库斯(Kusy)和茨姆巴(Ziemba)于1986年为温哥华积蓄信贷协会的5年资金规划期设计出的一个简单弥补的多期随机线性规划模型,极大地助推了商业银行ALM理论的研究。在库斯-茨姆巴模型之后,ALM理论的另一转折点式的贡献是卡里罗(Carino et al)等创建的Russell-Yasuda Kasai模型。Russell-Yasuda Kasai模型在日本Yasuda保险公司(Yasuda公司)执行试图性运用,使该公司在满足账面价值规则及条例管制的同期,能遵循公司的经济价值,而且,该模型还可以对与公司业务环境有关联的事件结果来执行资产配置和负债管理决策,清除将来资产负债价值的未知性。在运用这一模型的两年内,即1991年和1992年,按这一模型设计的投资策略,使Yasuda公司得到了7900万美元的额外收益。 (二)随机控制方法以状态的接连统(continuum)表明不确定状态,接连统的特质以少量服从联合马尔可夫过程的状态向量描述 。Brennan et al.分析了可以在债券、股票和现金方面投资的投资管理困难,假定有三个状态变量影响期望资产回报的时间改变,这三个变量即短时间利率(r)、长期债券利息率(l)及股票资产组合分红收益(δ)。该文假定投资人没有负债,假定负债的期望上涨率依靠于状态变量的水准,将负债包含进去相对来看很简单直接。如前所述,状态向量服从联合马尔可夫过程,该过程如果为下方形式: dr = μrdt + σrdzr dl = μldt + σldzl dδ − μδdt + σδdzδ 股票与债券由下式给定:
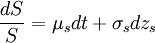 ALM
ALM
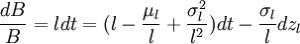 ALM
ALM
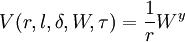 ALM
ALM
定义x为组合中股票的比例,y为康索尔债券的比例,Bellman方程为:
maxx,yE[dV] = 0 解其一阶条件,可以寻到最优控制解x * (r,l,δ,τ)和y * (r,l,δ,τ),该过程可以由经验报告预期,投资人的最优控制困难可以通过参数值的预期得到处理。 Brennan和Schwartz[1]通过允许投资人在短时间利率期货如股票、债券或现金上采取长线或短线的情形扩展了这个模型,通过分析,他们觉得如此的投资机会可以明显改观期望效用。其余一部分研究人士利用这个理论讨论了大学捐赠基金的优化投资策略困难等[2]。 随机规划与随机控制ALM模型的评析 随机规划ALM模型事实上是一类模型,它给予了模拟一般目标的方法。这些目标可以包含交易费用、税费、法律政策制约等方面的要求。受于考虑了大量原因,模型的变量逐渐增多,进而致使大批的优化困难,其计算成本相当高,因此实用性让人怀疑。我们以“机会制约模型(Chance Constrained Model)”为例。 机会制约模型最早由Charnes和Kirby提出 。在他们的论文里,将将来的存款与贷款开支看作是联合分布的随机变量,以资本足够率公式作为机会制约。该模型的缺点是,违背约束的情形并没有依据其数量予以惩罚。Charnes等将该方法应用于资产负债表的管理,此外两篇文章用该模型对保险公司的资产组合执行分析。 Dert在指定收益年金领域将该模型发展为多阶段机会制约模型(Multistage chance-constrained ALM model),与Charnes和Kirby不同的是,该作者以场景模拟未知性并非是作分布如果。以该模型为例,该这个模型的目标函数是,在失去偿付能力的风险水平可以接受、保证及时支付指定收益的能力的平稳性的制约下达到筹资成本最小。其中偿付能力要求为基金余下负债与相应偿付能力比率的乘积,资产价值差于要求的水准通过场景设定模拟。